Die Kapazität eines Kondensators (Protokoll)

1) Einführende Worte zum Thema

Messung der aufgenommenen Ladung Q in Abhängigkeit von der Spannung U:ge

Messung der aufgenommenen Ladung Q in Abhängigkeit von der Spannung U::

Dieses Versuchsprotokoll behandelt die Messung der Kapazität eines Kondensators, einem elektrischen Bauelement, das die Fähigkeit besitzt, elektrische Ladung zu speichern. Die Kapazität eines Kondensators ist ein bedeutender Parameter, der von verschiedenen Einflussfaktoren abhängt. Die Kapazität gibt an, wie viel Ladung der Kondensator pro Volt aufnehmen kann. Um die Auswirkungen unterschiedlicher Parameter auf die Kapazität eines Kondensators zu untersuchen, wurden eine Reihe von Experimenten durchgeführt.

2) Vermutungen bezüglich der Auswirkungen der Parameter:

• Plattenabstand (d): Es wurde vermutet, dass ein reduzierter Plattenabstand zu einer erhöhten Kapazität führt.

• Plattenfläche (A): Es wurde vermutet, dass eine größere Plattenfläche die Kapazität erhöhen könnte, da eine größere Fläche mehr Raum für die Speicherung von Ladungen bieten würde.

• Spannung (U): Es wurde vermutet, dass das Verhältnis von Spannung und Ladung entscheidend für die Menge der Ladung, die auf einem Kondensator gespeichert wird. Eine erhöhte Spannung führt dazu, dass mehr Ladung auf dem Kondensator gespeichert wird.

Diese Annahmen dienen als Grundlage für unsere weiteren Untersuchungen und Messungen.

3) Experimente:

Material:

1. Spannungsquelle
2. Messwiderstand
3. Plattenkondensator
4. Messverstärker

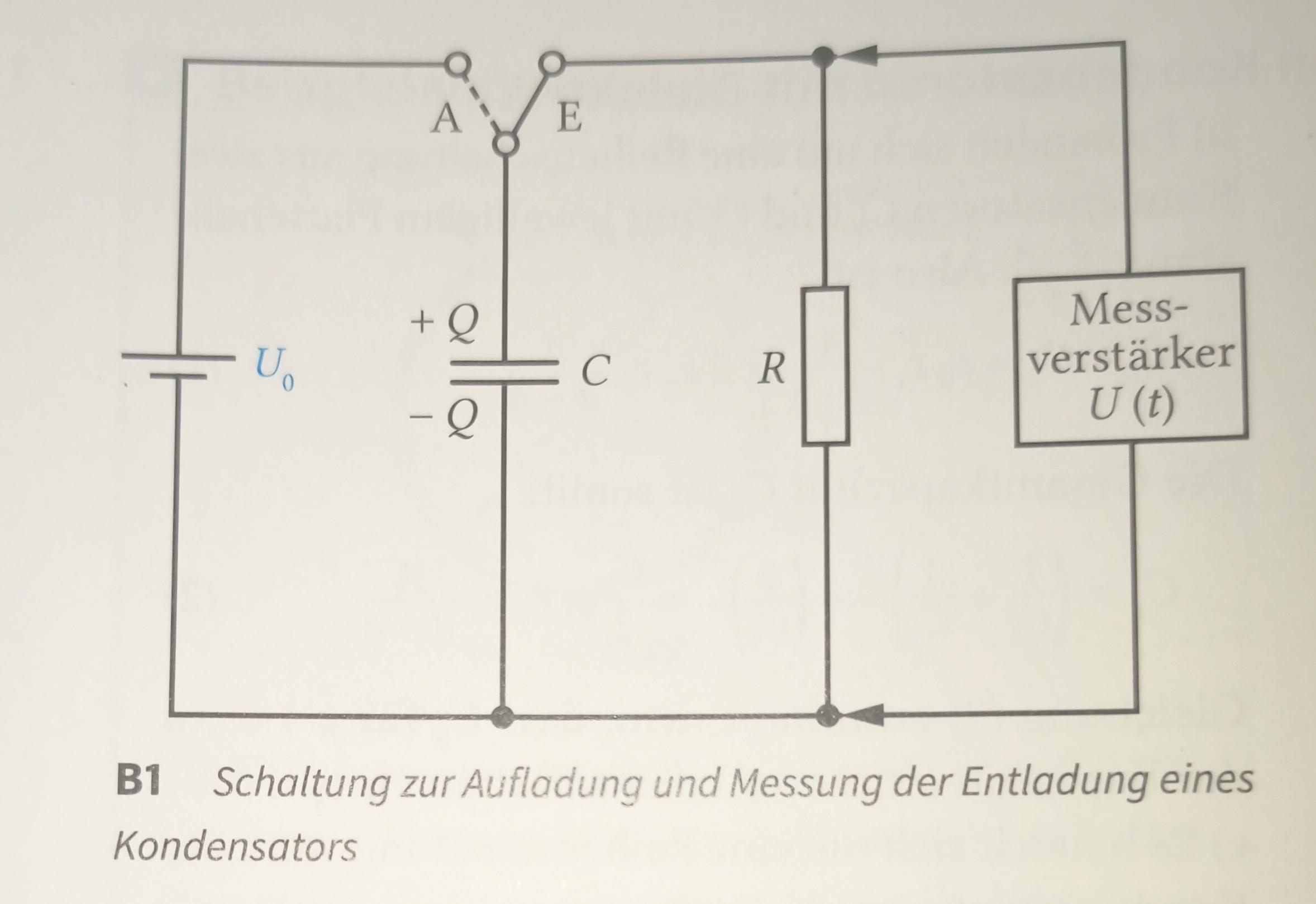
Skizze:

Messung der aufgenommenen Ladung Q in Abhängigkeit von der Spannung U:

Durchführung:

Eine Platte des Kondensators wird mit der Spannungsquelle und dem Messverstärker mit der gemeinsamen Erde verbunden. Die andere Platte wird durch Berühren mit Kabel 1 am Messwiderstand geladen und schließlich durch Berühren mit Kabel 2 über den ladungsempfindlichen Messverstärker entladen.

Messung:

Messreihe	Wert 1	Wert 2	Wert 3	Wert 4	Wert 5	Wert 6	Wert 7	Wert 8	Wert 9	Wert 10
Q in mC	0	6	12	17	23	25	35	42	47	52
U in V	0	100	200	300	400	500	600	700	800	900

Auswertung:

• Anhand des Graphen und der Messwerte wird deutlich, dass eine lineare Funktion vorliegt.

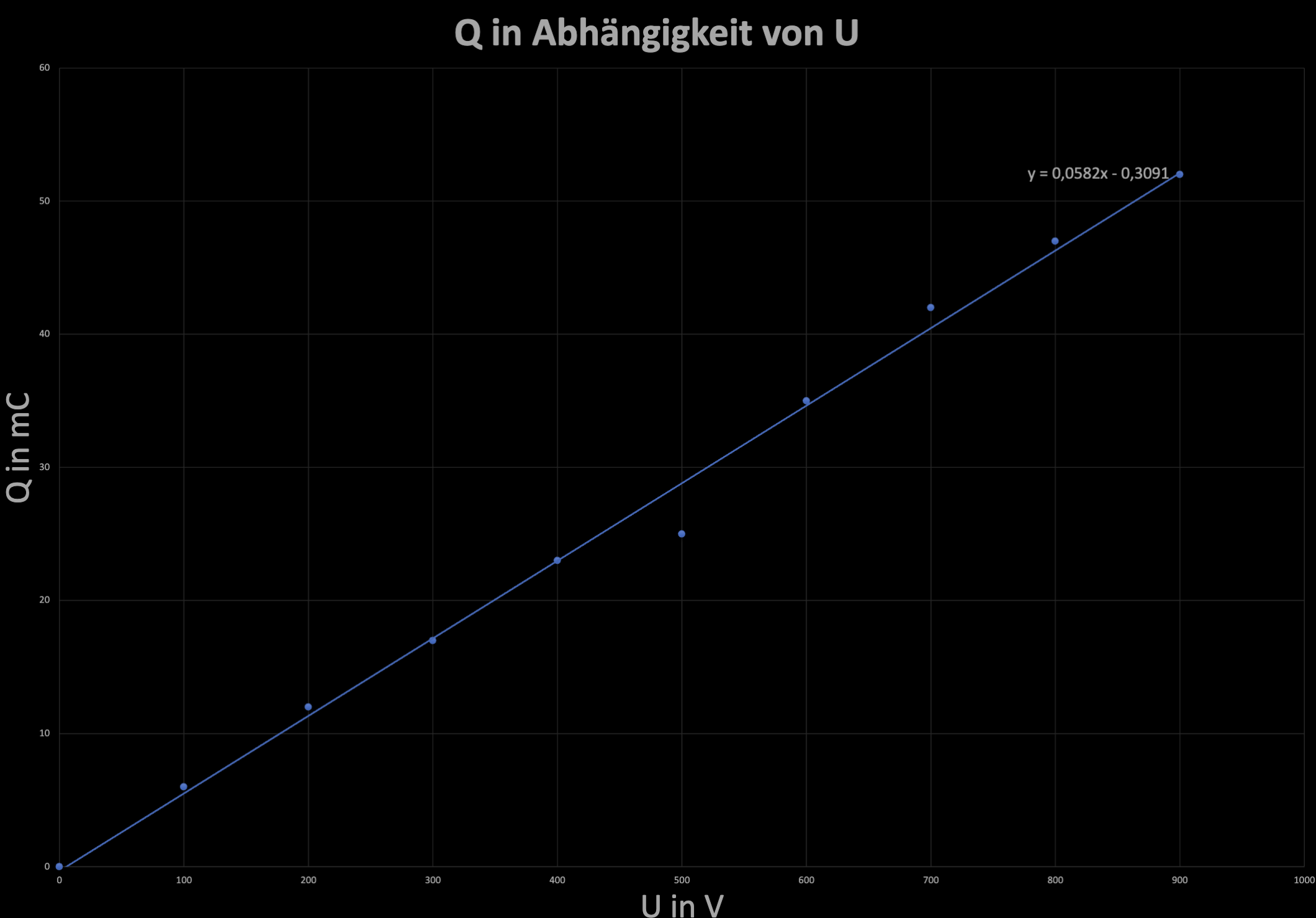
Mathematischer Zusammenhang:

$y=0.0582x-0,3091$

physikalischer Zusammenhang:

$Q=0,0582\cdot \frac{C}{V}\cdot U-0.3091C$ Daraus folgt: $Q\propto U$

Formel

Die Einheit von Kapazität (C) ist Farad (F):

$C(Kapazit\ddot{a}t)=Farad(F)=\frac{\Delta Q}{\Delta U}=\frac{C}{V}$

Messung der Kapazität C in Abhängigkeit von der Plattenfläche A:

Durchführung:

Der vorherige Versuch wurde mit einem festen Plattenabstand von 2mm, aber mit unterschiedliche Flächen der Kondensatorplatten wiederholt.

Messung:

Messreihe	Wert 1	Wert 2	Wert 3	Wert 4	Wert 5	Wert 6	Wert 7	Wert 8	Wert 9
UinV	200	200	200	200	200	200	200	200	200
Q in 10⁻⁸ C	0.44	0.88	1.3	1.78	2.22	2.66	3.1	3.54	3.98
A in cm²	50	100	150	200	250	300	350	400	450
C in 10⁻¹² F	22	44	65	89	111	144	155	177	199

Auswertung:

• Anhand des Graphen und der Messwerte wird deutlich, dass eine lineare Funktion vorliegt.

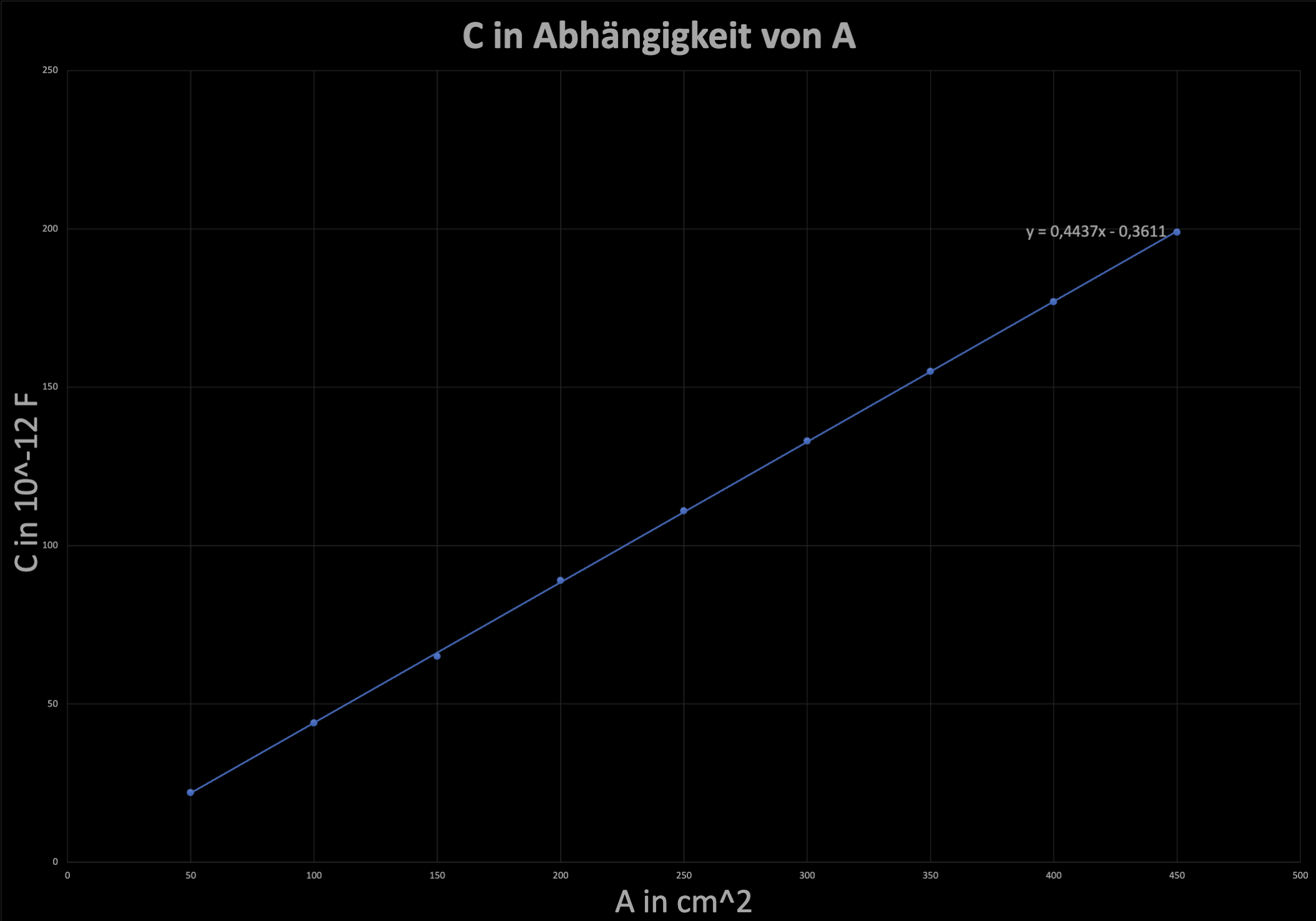
Mathematischer Zusammenhang:

$y=0.4437x-0,3611$

physikalischer Zusammenhang:

$C=0.4437\cdot \frac{10^{-12}F}{c{m}^2}\cdot A-0.36111\cdot 10^{-12}F$ Daraus folgt: $C\propto \epsilon \cdot A$

Messung der Kapazität C in Abhängigkeit vom Plattenabstand d:

Durchführung:

Der vorherige Versuch wurde mit einer festen Plattengröße von 450 cm², aber mit unterschiedlichem Plattenabstand zwischen den Kondensatorplatten wiederholt.

Messung:

Messreihe	Wert 1	Wert 2	Wert 3	Wert 4	Wert 5	Wert 6	Wert 7	Wert 8	Wert 9
U in V	200	200	200	200	200	200	200	200	200
Q in 10^-8 C	8	4	2.66	2	1.6	1.33	1.142	1	0.88
d/mm	1	2	3	4	5	6	7	8	9
C in 10⁻¹² F	400	200	133	100	80	66.5	55.71	50	44

Auswertung:

• Anhand des Graphen und der Messwerte wird deutlich, dass ein Hyperbel vorliegt.

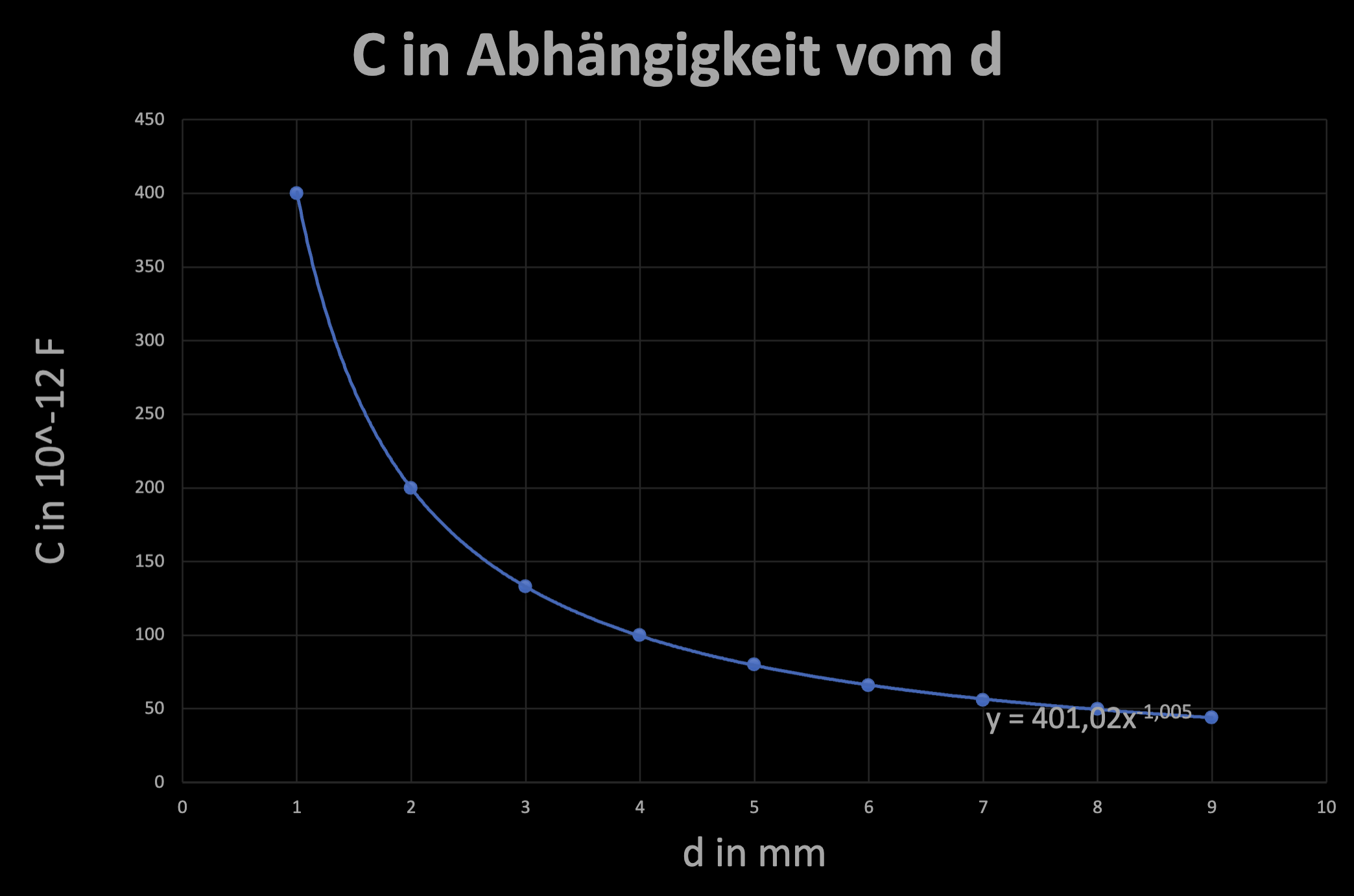
Mathematischer Zusammenhang:

$y=401,02x^{-1,005}$

physikalischer Zusammenhang:

$C=401,02\cdot \frac{mm}{10^{12}F}\cdot \frac{1}{d^{1,005}}$ Daraus folgt: $C\propto \frac{1}{d}$

Bestimmung der Proportionalitätskonstante:

Es wurde aus den vorherigen Versuche festgestellt, dass:

$C\propto \epsilon \cdot A\cdot \frac{1}{d}$

Daraus folgt: $C\propto \epsilon \cdot \frac{A}{d}$

Proportionalitätskonstante: $\epsilon =\frac{c\cdot d}{A}$

Berechnung der Proportionalitätskonstante:

Es wurde zwei verschiedene Werte von zwei verschiedenen Tabellen genommen, um die Proportionalitätskonstante zu berechnen.

1. $k=\frac{c_1\cdot d_1}{A_1}=\frac{22\cdot 10^{-12}F\cdot 2\cdot 10^{-3}m}{0.005m^2}=8.8\cdot 10^{-12}$
2. $k=\frac{c_2\cdot d_2}{A_2}=\frac{44\cdot 10^{-12}F\cdot 9\cdot 10^{-3}m}{0.045m^2}=8.8\cdot 10^{-12}$

Die elektrische Feld konstante für einen Luftgefüllten Kondensator: $k=8.8\cdot 10^{-12}\frac{A\cdot s}{Vm}$

Formel:

Aus der letzten zwei Versuchen und die Proportionalitätskonstante, ergibt sich folgende Formel: $C(Kapazit\ddot{a}t)=\epsilon \cdot \frac{A}{d}$

Relative Dielektrizitätszahl

In einem abschließenden Versuch wurde ein Kondensator mit einem Plattenabstand von 4 mm und einer Plattenfläche von 800 cm² verwendet. Zwischen den Kondensatorplatten wurde abwechselnd eine Kunststoffplatte und eine Glasplatte platziert. Durch die Anwendung der Dielektrizitätskonstanten-Formel und die Auswertung der Messergebnisse wurde das Verhältnis zwischen der Kapazität des Kondensators mit den eingelegten Dielektrika und der Kapazität ohne Dielektrika ermittelt.

Messreihe:

Dielektrikum	Spannung (U)	Ladung (Q)	Kapazität (C)
Luft	100 V	20 · 10⁻⁹ As	2 · 10⁻¹⁰ F
Polystyrol	100 V	31 · 10⁻⁹ As	3,1 · 10⁻¹⁰ F
Glas	100 V	82 · 10⁻⁹ As	8,2 · 10⁻¹⁰ F

Auswertung:

Mit Hilfe der Messreihe wurde das Verhältnis zwischen der Kapazität des Kondensators mit den Dielektrika Polystyrol oder Glas und der Kapazität des Kondensators ohne Dielektrikum (Luftkondensator) untersucht. Die Ergebnisse dieses Versuchs sind wie folgt:

• Relative Dielektrizitätszahl von Glas: $\frac{C_{Glas}}{C_{Luft}}=\frac{8,2\cdot 10^{-10}F}{2\cdot 10^{-10}F}=4,1{\epsilon }_r$

• Relative Dielektrizitätszahl von Polystyrol: $\frac{C_{Polystyrol}}{C_{Luft}}=\frac{3,1\cdot 10^{-10}F}{2\cdot 10^{-10}F}=1,55{\epsilon }_r$

Basierend auf diesen Ergebnissen ergibt sich die Formel für Kondensatoren mit Dielektrika (Füllung): $C=\epsilon \cdot {\epsilon }_r\cdot \frac{A}{d}$ wobei $\epsilon$ für die elektrische Feldkonstante steht und entspricht $8,854188\times 10^{-12}As/Vm$ und ${\epsilon }_r$ für die Dielektrizitätskonstante.

4) Zusammenfassung der Ergebnisse:

Kondensator kann elektrische Ladung Speichern und freigeben.

Plattenabstand (d):

• Bei kleinerem Plattenabstand sind die elektrischen Feldlinien dichter (elektrische Feldstärke wird größer) und die Kapazität erhöhte sich. $C=\frac{Q}{U}=\frac{{\epsilon }_0\cdot {\epsilon }_r\cdot A}{d}$ Plattenfläche (A):
• Eine Erhöhung der Plattenfläche führte zu einer proportionalen Steigerung der Kapazität. Dies resultierte aus der Tatsache, dass größere Plattenflächen mehr Raum für die Speicherung von Ladungen bieten.

Relative Permittivität eines Dielektrikum bzw. Faktor der Kapazität(${\epsilon }_r$): ist das isolierende Material zwischen den Kondensatorplatten.

• Eine höhere relative Permittivität  ${\epsilon }_r$  führt zu einer erhöhten Kapazität. Dies geschieht durch die Polarisation innerhalb des Dielektrikums, wobei sich die Ladungen im Material so verschieben, dass ein entgegengesetztes elektrisches Feld zum ursprünglichen Feld des Kondensators entsteht. Dieses interne Feld verringert die resultierende elektrische Feldstärke zwischen den Platten. Dadurch kann sich bei konstanter Spannung $U$ mehr Ladung auf den Platten ansammeln, was zu einer höheren Kapazität führt. Dies ermöglicht dem Kondensator, insgesamt mehr Energie zu speichern, was für viele technische Anwendungen vorteilhaft ist.
• Hints: Mann stillt sich das so vor, als ob Vakuum ${\epsilon }_r=1$ hat. Im Vakuum gibts aber nichts was Polarisiert werden kann, darum wenn ein anderer Isolator gebracht wird, entsteht Polarisation durch das elektrische Feld des Kondensators, was durch die angelegte Spannung zustande kommt.

Flächenladungsdichte ( $\sigma$): 

• Es gibt an, wie viel elektrische Ladung pro Flächeneinheit auf einer Kondensatorplatten gespeichert ist. $\sigma =\frac{Q}{A}={\epsilon }_0\cdot {\epsilon }_r\cdot E={\epsilon }_0\cdot {\epsilon }_r\cdot \frac{U}{d}$ wobei:
  • $\sigma$ die Flächenladungsdichte ist, in ${\text{C/m}}^2$
  • $Q$ die Ladung auf einer der Kondensatorplatten ist, in $\text{C}$
  • $A$ die Fläche einer Kondensatorplatte ist, in ${\text{m}}^2$
  • ${\epsilon }_0$ die elektrische Feldkonstante (Permittivität des Vakuums) ist, mit
    • ${\epsilon }_0\approx 8,85\times 10^{-12},\frac{{\text{C}}^2}{\text{N}\cdot {\text{m}}^2}$
  • ${\epsilon }_r$ die relative Permittivität des verwendeten Dielektrikums ist (dimensionslos)
  • $E$ die elektrische Feldstärke im Kondensator ist, in $\text{V/m}$ oder $\text{N/C}$
    • $E=\frac{U}{d}$
  • $U$ die Spannung zwischen den Kondensatorplatten ist, in $\text{V}$
  • $d$ der Plattenabstand ist, in $\text{m}$.
  • $C$ die Kapazität von einem Kondensator ist, (Farad in F)

Energie des geladenen Kondensators (Elektrische Feld Energie):$E=\frac{1}{2}\cdot C\cdot U^2$ Wenn die Platten eines isolierten Kondensators auseinandergezogen werden, sinkt die Kapazität, die Spannung steigt (da die Ladung konstant bleibt), und dadurch steigt die gespeicherte Energie, weil die Energie im Kondensator proportional zum Quadrat der Spannung ist.

Der Unterschied zwischen Flächenladungsdichte und die Kapazität in der Formel ist nur durch den Ersatz von $U$ mit $A$.